우연히 한 인터넷 페이지를 보고 놀라웠다. (http://mathnotes.tistory.com/181)

한 옥타브는 왜 12개의 음으로 구성되어 있을까?

한 옥타브는 C, C#, D, D#, E, F, F#, G, G#, A, A#, B 으로 되어 있다.

(그림출처: http://imgv.search.daum.net/viewer/search?w=imgviewer&SearchType=total&ResultType=total&SimilarYN=total_Y&SortType=total&q=%C7%C7%BE%C6%B3%EB%20%B0%C7%B9%DD%20%B1%D7%B8%B2%20%B5%B5%B7%B9%B9%CC%C6%C4%BC%D6%B6%F3%BD%C3&sidx=0&lpp=10&uk=USwKi697@44AAHVfT7YAAABA&mk=UedVmm4t1AwAABr3UCoAAAE4)

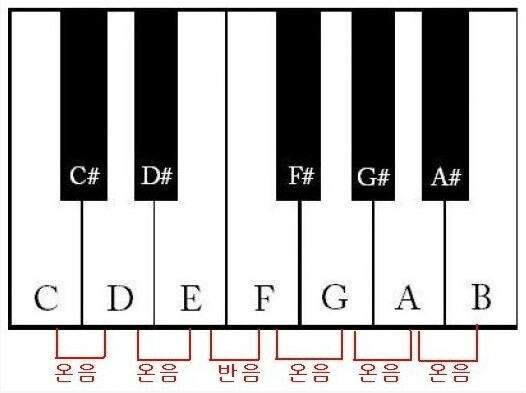
피아노 건반에  있는 7개의 하얀 건반은 C, D, E, F, G, A, B(도, 레, 미, 파, 솔, 라, 시)이고 그 사이에 있는 5개의 검은 건반은 C#, D#, F#, G#, A#이다. (그런데 왜 '도'가 알파벳 첫글자 A가 아니고 'C'일까?)

위 페이지의 내용을 요약하면 아래이다 (수학적인 내용 있음).

음은 주파수의 의해 결정된다. 

어떤 주파수는 그것의 2 배인 주파수와 어울린다(두 음을 동시에 들을 때 편하다. 예, 300Hz와 600Hz).

하지만 어떤 주파수와 그것의 3배인 주파수를 동시에 들으면 불편하다(예, 300Hz와 900Hz).

(위 사이트에 가면 실제로 그 음을 들을 수 있다. 2배는 편하지만 3배는 불편함을 귀로 확인할 수 있다)

그래서 어떤 주파수와 그것의 1.5배(3배/2)인 주파수를 동시에 들어봤더니 그런대로 편안하다(예, 300Hz와 450Hz). 그런데 어떤 주파수와 그것의 1.5배인 주파수는 '완전 5도'라고 불려지는 화음이라고 한다. 도와 솔은 완전 5도이다. 그런데 우리가 실제로 듣고 있는 도와 솔은 완전 5도가 아니다. 왜? 그 비율이 1:1.5가 아니라 1: 1.498이므로. 왜 그럴까?

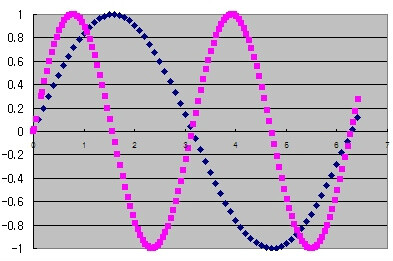
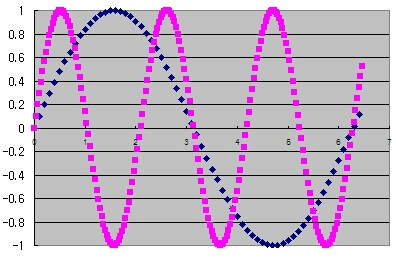
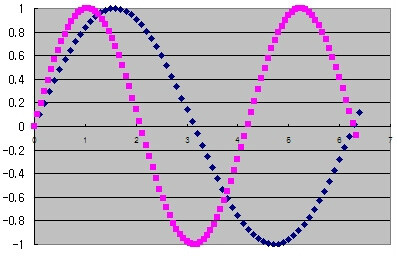
하여튼 계속 이 작업을 해보자. 우리는 지금까지 어떤 주파수와 그 주파수의 2배인 주파수 안에서(예, 300Hz ~ 600Hz) 편안한 주파수(음)를 찾고 있다. 그래서 지금까지 찾은 것인 2배, 1.5배이다.

1.5배를 3배하면 4.5배이다. 4.5배를 2로 나누면 2.25배이다. 우리는 1과 2배 사이의 음을 찾고 있는데 2.25배는 2배보다 크므로 다시 2로 나누면 1.125배가 된다. 

(위의 인터넷 페이지에는 1.5배와 1.125배가 완전 5도라고 하는데 나는 그것이 이해가 안된다. 완전 5도라면 1: 1.5 의 비율이어야 하는데 1.5와 1.125는 1: 1.3333.. 이기 때문이다.)

이 작업을 계속 하면(이전 음을 3배해서 2보다 작을 때까지 나누기 2 하는 작업), 1.125 다음은 1.6875가 된다. 1.125와 1.6875는 는 1: 1.5 비율이므로 '완전 5도'가 된다. 

이렇게 이전 음과 완전 5도가 되는 음를 찾는 작업을 계속 진행하다 보면 이전에 나온 음이 다시 나오기를 기대하게 된다. 그래서 어떤 순환이 만들어지기를 기대하게 된다. 하지만 불행하게도 이 작업은 무한하다고 한다.ㅠㅠ 

우리의 작업을 수학으로 표현하면, 1.5^n = 2^m (예, p(m)=2^(m/n)) (^: 지수표현)

1.5는 완전 5도의 비율(1:1.5)이고 2는 나누기 2이다.

n은 한 옥타브(스케일)를 구성하는 음들의 수이고 m은 0 부터 n-1 까지 변하는 수이다.

이전까지의 방식으로는 유한 개의 옥타브를 만들 수 없다. 그래서 우리의 전략을 수정한다. 완전 5도가 되는 비율인 1: 1.5를 양보하는 것이다. 유한 개의 옥타브를 얻을 수 있다면 1.5가 아니라 1.5의 근사치만 되더라도 그게 낫다는 것이다. 적당한 타협이다.

1.5^n = 2^m (예, p(m)=2^(m/n)) 에서 n = 12로 고정하면 아래의 표를 얻을 수 있다.

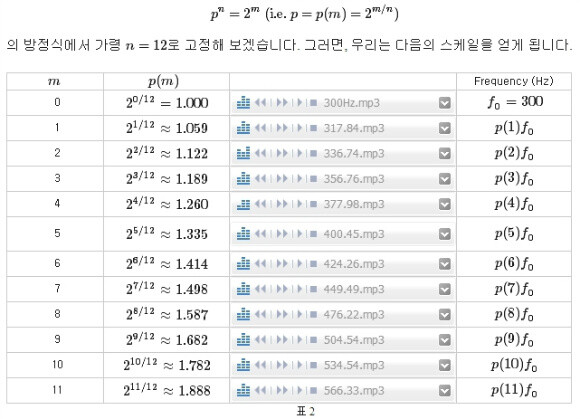
(2의 1/12승이라.. 저걸 어떻게 계산하냐구.ㅠㅠ 12번 제곱해서 2가 되는 수를 어떻게 찾냐(답은 1.059..지만). 어렵다. 공학용 계산기를 두드려봐야 할 듯.)

위 표를 보면 m=0 과 m=7 에서 p(m)의 비율이 1: 1.489이다. 1:1.5는 아니지만 1: 1.5에 아주 가깝다. m=0은 '도'이고 m=7은 '솔'이다(m=1, 3, 6, 8, 10은 반음이다). 위의 표에 있는 것이 현재 사용하고 있는 12음계이다. 그래서 악기를 만들 때나 음악을 만들 때 완전 5음의 비율인 1: 1.5가 아니라 1: 1.498로 맞춘다고 한다!

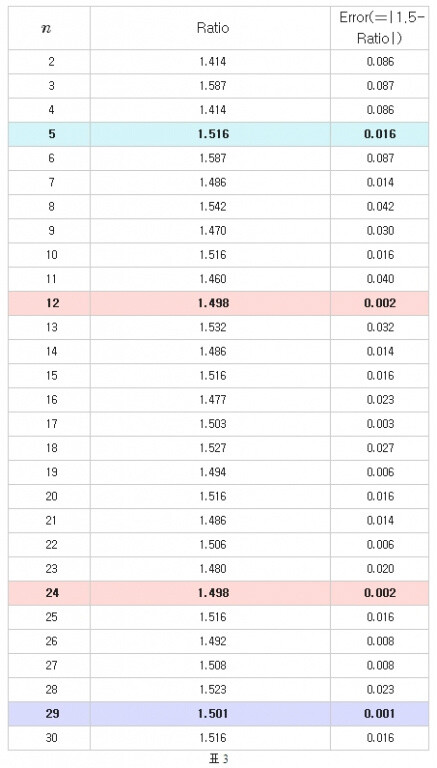
위 표는 n이 다양할 때이다. 완전 5도의 비율인 1.5에 근접한 n은 5, 7, 10, 12, 14, 16, 17, 19, 20, 21, 22, 24, 25, 26, 27, 29, 30입니다. 완전 5도의 비율에 가장 가까운 n은 29이고(0.001) 두 번째로 가까운 n은 12와 24이다. 한국에서 쓰는 5음계(7성음계에서 2개를 뺀 것, 궁상각치우. 도레미솔라에 해당)는 n=5인 경우입니다. 옛 사람들도 '완전 5도'가 듣기 편하고 좋다는 걸 알고 있었나 보다.

제가 제대로 이해한 것인지 모르겠지만 왜 12개음인지 알게 되어 기쁘다!ㅎㅎ

---------------

사진을 빛과 시간의 예술이라고 한다. 사진에서 빛과 시간이 중요한 요소이기 때문이다. 셔터스피드는 시간을 조절하고 조리개는 빛을 조절한다. 빛과 시간에 의해 사진은 결정된다. 사진은 빛과 시간의 기록이라고 할 수 있다. 색을 만들어내고 색을 결정하는 것은 빛이다. 색은 그 물체가 뿜어내는 것이 아니라 빛이 그 물체에 반사되어 튕겨나온 것이다. 즉 빛이 있어야 색이 존재할 수 있다. 빛은 색의 어머니이다. 밤에 달이 빛나는 이유는 달이 스스로 빛을 내는 게 아니라 태양빛이 반사되기 때문인 것처럼. 달빛의 어머니는 태양이다.

음악은 주파수와 시간의 예술이라고 생각한다. 음의 높낮이는 주파수로 결정된다. 수많은 주파수들 중에서 조화로운 12개음을 정해서(완전 5도를 기초로) 그것을 바탕으로 음악이 만들어진다. 그리고 당연히 음악에서 박자, 빠르기가 중요하다. 음의 높낮이를 정하는 주파수와 음의 지속기간을 정하는 시간은 음악에서 중요한 요소이다. 이 두 요소로 음악이 결정된다고 할 수 있다.

지금 우리가 살고 있는 세계는 시간과 공간이 결정한다. 사진이나 음악이나 이 세계나 '시간'은 공통적으로 중요한 요소이다. 그리고 사진은 '빛'이 있고 음악에는 '주파수'가 있고 이 세계에는 '공간'이 있다. 어찌 보면 이 세계의 '공간'에 해당되는 요소가 사진에서 '빛'이고 음악에서 '주파수'인 것 같다. 즉, 사진에서의 '빛'과 음악에서의 '주파수'는 공간적인 요소라고 할 수 있다. 

그런데 빛도 주파수의 일종이다. 빛은 전자파의 일종이라고 알려져 있다(750 ~ 400THz, 상당히 높은 주파수다). 빛은 넓은 주파수 대역을 가지고 있는데 사람의 눈에 보이는 대역을 '가시광선' 대역이라고 한다. 흔히 말하는 '빨주노초파남보'다. 이 가시광선 대역 보다 낮은 대역이 적외선 대역이고, 높은 대역이 자외선 대역이다. 적외선에서 '적'은 빨간색을 의미하고 빨간색쪽에 있다는 것이고, 자외선에서 '자'는 자주색을 의미하고 자주색쪽에 있다는 것이다(자주색과 보라색은 비슷한 색이다). 

소리도 주파수의 일종이다. 사람이 들을 수 있는 주파수를 '가청주파수' 대역이라고 한다(20 ~ 20kHz). 돌고래는 사람이 들을 수 없는 저주파로 의사소통한다는 얘기가 있다. 

물체도 고유 주파수가 있다고 한다. 이 세계의 공간을 이루는 다양한 요소들. 물, 공기, 구름, 새, 식물, 산, 흙, 불, 사람, 동물, 작은 생명들 등은 모두 고유의 주파수를 가지고 있다. 그런 의미에서 이 세계의 공간을 주파수들의 모음이라고 단순화시킬 수 있다. 

이렇게 생각해보면, 사진도, 음악도, 이 세계도 시간이라는 공통된 요소와 별개로 '주파수'라는 공통된 요소를 갖게 된다. 색들을 주파수로 나타낼 수 있고 소리들을 주파수로 나타낼 수 있다. 그리고 우리가 사는 3차원의 공간 역시 주파수로 나타낼 수 있다고 생각한다 (좀 억지스러운 면이 있지만). 

우리가 인식하지 못하는 주파수 대역들이 있다. 엄청나게 광대한 대역들이다. 가시광선과 가청주파수 이외의 대역들. 그 안에는 무슨 정보들이 있을까? 그 안에는 어떤 것들이 있을까? 우리가 보고 듣는 것은 주파수 세계에서 빙산의 일각에 불과할 것이다. 물론 우리는 주파수를 이용하여 라디오를 듣고 TV를 보고 핸드폰으로 통화하고 레이다를 돌리고 위성통신을 하고 전자레인지를 돌리는(물의 공진주파수인 2.45GHz 이용) 등을 한다. 하지만 그런 것들을 다 합쳐도 빙산의 일각일 것이다. 인간이 모르고 있는 주파수대에 뭐가 있는지 궁금하다. 그냥 모르는 게 약일까!

(2013-07-18 밤에 추가)

---------------

<참고>

http://mathnotes.tistory.com/181

http://blog.daum.net/bs2158/17443213