만나는 평행선 위에서 유클리드의 산책

 

이 그림은 <유클리드의 산책>이라는 작품입니다. 유리창 너머 산책길 위에 점 두 개가 보이시죠? 두 사람이 산책하고 있는 모습을 그린건데, 너무 멀어서 사람이 마치 개미처럼 보입니다. 여기 한 사람이 바로 선생님이고, 또 다른 한 사람이 바로 접니다.

 

‘평행선은 결코 만날 수 없다’를 주장하신 선생님이 만나는 평행선 위에 서 있는 모습이 재밌지요? 저는 이렇게 원근법을 이용해 ‘수학의 역설’을 표현하고 싶었습니다. 그래서 창 밖에 보이는 원뿔 모양의 탑과 산책길을 한 화면에 그렸지요. 평행선으로 이뤄진 산책길도 원뿔처럼 한 점에서 만날 수 있다는 걸 표현하기 위해서예요. 원근법이란 가까운 물체는 크게, 멀리 있는 물체는 작게 그리는 회화 기법입니다. 우리가 살고 있는 3차원의 공간을, 종이와 같은 2차원 평면 위에 그릴 때 쓰이죠. 원근법이 있기 때문에 거리와 깊이를 평면 위에 표현할 수 있답니다.

 

 

 

 

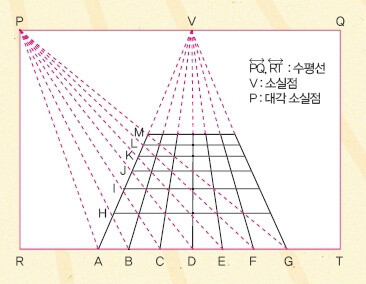
수학을 사랑했던, 르네상스의 화가들

 

원근법의 시작은 르네상스 시대로 거슬러 올라간다. 초기 원근법은 수학적인 비례가 정확하게 맞지 않았다. 그러다 1410년, 이탈리아의 건축가 필리포 브루넬리스키가 교회 건물의 밑그림을 그리다 사물의 크기를 거리에 따라 정확히 비례하게 그리는 방법을 알아냈다. 시선과 평행한 모든 직선이 수평선 위의 한 점(소실점)에서 모이도록 하여, 거리에 따른 비례에 맞게 사물을 그리기 시작한 것이다. 이때 눈 높이에 소실점이 오도록 하고, 소실점에서 *대각 소실점 까지의 거리만큼 작품과 떨어져 감상하면 작품의 입체감을 더욱 살릴 수 있다.

 

이후 유럽의 화가들은 치밀한 계산을 통해 감상자의 실제 눈높이와 소실점을 일치시켜 원근감의 효과를 강조하기 시작했다.

 

한편 이탈리아 화가인 피에로 델라 프란체스카는 원근법의 매력에 빠져, 이에 관련된 수학을 본격적으로 연구했다. 그는 1474년에 발표한 <회화의 원근법에 관하여>를 포함해 수학 논문을 세 편이나 쓰고, 화가이자 수학자로 활동을 이어갔다. 그의 논문에는 ‘3차원 공간을 2차원에 담기 위해 표현하는 입체감은 정확한 비례식을 따라야 한다’고 적혀 있다.

 

 

 

 

 

 

 

 

 

 

 

 

진실을 숨기는 왜상 화법

 

이 작품은 1533년 독일의 화가 한스 홀바인이 그린 <대사들>이다. 초상화가로서 재능이 뛰어났던 홀바인은 어느 날, 장 드 댕트빌 대사로부터 자신의 저택에 걸어둘 초상화를 그려 달라는 주문을 받는다. 몇 주 뒤 홀바인은 댕트빌 대사와 그의 친구인 조르부 드 셀브 주교의 모습을 실제 크기로 그려 초상화를 완성한다. 이 초상화에는 두 주인공들이 수학적인 도구와 수학책, 악기들이 널린 가구에 기댄 모습으로 그려져 있다.정치와 종교는 지식을 기초로 운영해야 한다는 뜻을 담기 위해서다.

 

한편, 그림 아래쪽 한가운데에는 분위기를 깨는 정체불명의 얼룩이 있다. 그 정체는 바로 해골! 하지만 이를 쉽게 알아보기 힘들다. 왜 그런 걸까?

 

해골을 왜상 화법으로 그렸기 때문이다. 해골은 평소 댕트빌의 좌우명인 ‘죽음을 기억하라!’를 상징한다. 댕트빌의 좌우명을 알고 있던 홀바인이 왜상 화법으로 초상화에 해골을 그려 넣어 작품에 의미를 더한 것이다. <대사들>에 그려진 해골을 보려면 그림의 오른쪽 끝을 앞으로 당겨 비스듬히 보면 된다.

 

 

 

 (중략)

 

 

착각을 부르는 미술관 셀린 들라보 저/김성희 역